Here in this article, we will derive the third equation of motion by graphical method. This equation relates initial and final velocity with acceleration and displacement. While solving problems you must remember that these equations can only be used when acceleration is constant. Here we will use v-t graph to derive the third equation of motion.
Formula for the third equation of motion
The third equation of motion is given by the relation
\(v^2=u^2+2as\)
Where,
\(v=\) final velocity,
\(u=\) initial velocity,
\(a=\) acceleration and
\(s=\) distance travelled.
Note: – This equation along with other kinematics equations of motion are valid for objects moving with uniform acceleration.
Derivation of 3rd equation of motion by graphical method
To derive the 3rd equation of motion we will make the following assumptions
- Object under consideration is moving with acceleration \(a\,\, m/s^2\)
- At time \(t=0\) object have some initial velocity. Let’s denote it by \(u\,\, m/s\)
- At time \(ts\) object have some final velocity. Let’s denote it by \(v\,\, m/s\)
- Total distance covered by object in time \(t\) seconds is \(s\) meters.
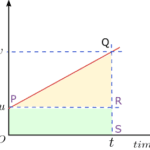
Object is moving with a uniform acceleration “a” along a straight line. The initial and final velocities of the object at time \(t = 0\) and \(t = t\,\, s\) are \(u\) and \(v\) respectively. During time \(t\), let \(s\) be the total distance travelled by the object.Figure given below show the velocity-time graph for the object whose initial velocity is \(u\) at time \(t=0\) and velocity \(v\) at time \(t\).
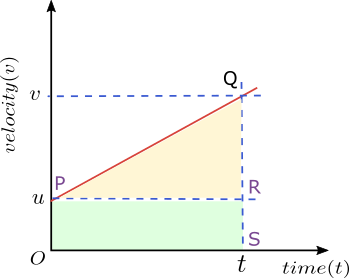
We know that the distance covered by the object moving with uniform acceleration is given by the area under the velocity-time graph. Here area under the velocity-time graph is equal to area of trapezium OPQS
∴ Area of trapezium OPQS \[= \frac{1}{2}\text{(Sum of Parallel Slides + Distance between Parallel Slides)}\]Or, \[s=\frac{OP+SQ}{2}\times PR\]
We have knowledge about acceleration of the moving object. So, Acceleration \[a=\frac{\text{Change in velocity}}{time}=\frac{QR}{PR}\]Or,\[PR=\frac{QR}{a}\]From graph we can see that \[QR=v-u\]\[t=PR=\frac{v-u}{a}\]From above figure we can see that\[OP=u\]\[SQ=v\]\[OP+SQ=u+v\]Substituting these values, we get\[s=\left(\frac{u+v}{2}\right)\times\left(\frac{v-u}{a}\right)=\frac{v^2-u^2}{2a}\]Rearranging it we get\[v^2=u^2+2as\]Which is third equation of motion.
Related Articles