The following are the important kinematics equations list. I will also provide a link to a Google Docs file from where you can download the file as a pdf (see at the end of the article).
Physics – Kinematics Equations
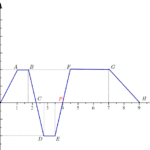
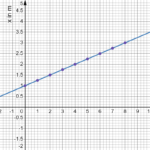
Average Velocity and speed
\[v_{avg} = \frac{\Delta s} {\Delta t} \\
\text{Average Speed} = \frac{\text{Total distance}}{\text{time taken}}
\]
learn more about average velocity
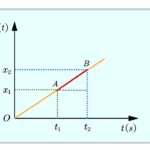
Instantaneous velocity and speed
$v = \mathop {\lim }\limits_{\Delta t \to 0} {{\Delta s} \over {\Delta t}} = {{ds} \over {dt}}$
Instantaneous speed or speed is the magnitude of the instantaneous velocity
where $s$ is the displacement of the object and has only one component(out of x, y, and z) for motion along a straight line and has two components for motion in a plane.
Learn more about the Difference between speed and velocity and practice the concept of speed and velocity at this Speed and Velocity Quiz
Average acceleration
$${a_{avg}} = {{\Delta v} \over {\Delta t}}$$
Instantaneous acceleration
$$a = \mathop {\lim }\limits_{\Delta t \to 0} {{\Delta v} \over {\Delta t}} = {{dv} \over {dt}}$$
Equations of motion (constant acceleration)
$$v = {v_0} + at$$ $$x = {x_0} + {v_0}t + {1 \over 2}a{t^2}$$ $${v^2} = {v_0}^2 + 2a(x – {x_0})$$ $$\overline v = {1 \over 2}(v + {v_0})$$
Free fall acceleration
$$v = {v_0} + gt$$ $$h = {v_0}t + {1 \over 2}g{t^2}$$ $${v^2} = {v_0}^2 + 2gh$$
Learn more about free fall in physics
Projectiles
Horizontal distance $$x = {v_x}t$$
Horizontal velocity $${v_x} = {v_{x0}}$$
Vertical distance $$y = {v_{yo}}t – {1 \over 2}g{t^2}$$
Vertical velocity $${v_y} = {v_{y0}} – gt$$
Here,
${v_x}$ is the velocity along the x-axis,
${v_{x0}}$ is the initial velocity along x-axis,
${v_y}$ is the velocity along the y-axis,
${v_{y0}}$ is the initial velocity along y-axis.
$g$ is the acceleration due to gravity and
$t$ is the time taken.
Time of flight $$t = {{2{v_o}\sin \theta } \over g}$$
Maximum height reached $$H = {{v_0^2{{\sin }^2}\theta } \over {2g}}$$
Horizontal range $$R = {{v_0^2\sin 2\theta } \over g}$$
Here,
$v_{0}$ is the initial Velocity,
${\sin \theta }$ is the component along y-axis,
${\cos \theta }$ is the component along x-axis.
Uniform circular motion
Angular velocity $$\omega = {{d\theta } \over {dt}}$$
where $\theta$ is the angle moved in radians
Relation between linear velocity, angular velocity, and radius of circular motion $$v=r\omega$$
Angular acceleration $$\alpha = {{d\omega } \over {dt}}$$
Centripetal acceleration $${a_c} = {{{v^2}} \over r}$$ $${{\vec a}_c} = – {\omega ^2}\vec r$$
Get the kinematics equation list as pdf (opens in new window)