Let us consider a projectile projected with initial velocity \(v_{0}\) making an angle \(\theta_0\) with the horizontal as shown below in the figure.
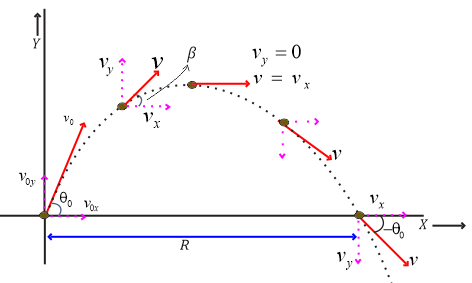
We know that the horizontal range of a projectile is the distance traveled by the projectile during its time of flight. This horizontal range is given by the relation \[\text{Horizontal Range}=\text{Horizontal velocity}\times \text{time of flight} \] So, the formula for the horizontal range is \[R=\frac{{v_0}^2 \sin 2\theta_0}{g} \qquad (1)\]
The maximum range for projectile motion
A projectile of the same mass can be launched with the same initial velocity and different angles \(\theta_0\).
Consider the figure given below where a projectile is launched with three different angles \(45^0,\,\,60^0,\,\,and\,\,30^0\).
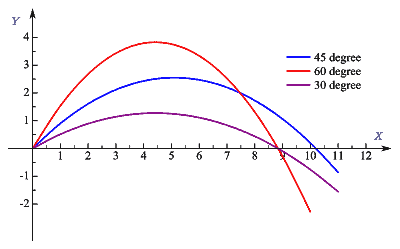
From the above figure, we can clearly see that for different angles of projection horizontal range of a projectile is different.
Let us now investigate the angle of projection for which range is maximum (note that initial velocity remains the same).
Learn more about velocity and speed
\[R=\frac{v_0 \sin 2\theta_0}{g} \] In above relation, if we keep initial velocity same for various launch , then value of \(R\) varies with the value of \(\sin 2\theta_0\).
Clearly, from trigonometry, we know that the maximum value of \(\sin \theta=1\) and we know that \(\sin 90^0=1\)
So in this case, we have
\(2\theta_0=90^0 \qquad or,\qquad \theta_0=45^0\)
Thus the horizontal range of a projectile for a given initial velocity is maximum when it is projected at an angle of \(45^0\) with the horizontal.
The maximum range of projectile formula
To find the formula for a maximum range put \(\theta_0=45^0\) in equation (1). So, from equation (1) we have
\[R_m=\frac{v_0^2 \sin 90^0}{g}=\frac{v_0^2}{g}\]
Question That can be asked from this topic
Question 1: Why do 45 degrees give a maximum range of a projectile?
Question 2: Prove 45 degrees maximum range for a projectile launched at an angle \(\theta\).
Question 3: Derive the formula for the range of projectile body launched at an angle \(\theta\).
