How to find the magnitude of an electric field?

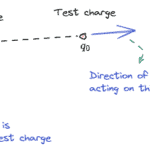
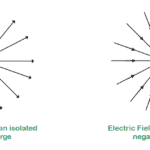
A field is a means of thinking about and visualizing the force that surrounds any charged object and acts on another charged object at a distance, even if there is no obvious physical contact between these two objects.

Electric field $E$ due to set of charges at any point is the force experienced by a unit positive test charge placed at that point.

The units of electric field are $N/C$ or $V/m$.

Electric field $E$ is a vector quantity meaning it has both

• magnitude and
• direction

In this article we will learn how to find the magnitude of an electric field.

Magnitude of electric field created by a charge

Let us now first look at finding magnitude of electric field created by a charge.

To find electric field due to a single charge we make use of Coulomb’s Law.

If a point charge $q’$ is at a distance $r$ from the charge $q$ then it will experience a force

$\vec{F}=\frac{1}{4\pi \epsilon_0}\frac{qq’\hat{r}}{r^2}$

Electric field at this point is given by relation

$\vec{E}=\frac{\vec{F}}{q’}=\frac{1}{4\pi \epsilon_0}\frac{q\hat{r}}{r^2}$

This is electric field at a distance $r$ from a point charge $q$ and $\hat{r}$ is the unit vector along the direction of electric field.

Above relation defining electric field at a distance $r$ tels about both magnitude and direction of the field.

Magnitude of electric field would be

$|\vec{E}|=\frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}$

In above equation you could notice the missing $\hat{r}$ part. This $\hat{r}$ tells us about the direction of the electric field. Since electric force is a central force and we have defined electric field using Coulombs law we can conclude that electric field acts along the line joining the charge $q$ (source point) and field point at which it is being measured.

This vector This $\hat{r}$ is known as unit vector of our displacement vector $\vec{r}$ and is given by relation

$\hat{r}=\frac{\vec r}{r}$

Where $r=|\vec{r}|$ which is the distance between our source point and the field point.

Solved Example 1

Find the magnitude of electric field at a distance $0.2m$ from a charge of $4nC$.

Solution

Step 1 – Figure out what is requited

The question asked us to find magnitude of electric field

Step – 2 Figure out information given in the question.

We are provided the magnitude of the charge as well as the distance between the field point and the charge.

Step 3- Find out the way to solve problem

We will use the relation

$E=k\frac{Q}{{r}^{2}}$

To find the magnitude of electric field.

Step 4- Solve the problem

$E=k\frac{Q}{{r}^{2}}$

where

$k=\frac{1}{4\pi\epsilon_0}=9.0\times 10^9 N\cdot m^/C^2$

So,

$E=(9.0\times 10^9)\frac{4\times 10^9}{{.2}^{2}}=900N/C$

Magnitude of electric field due to multiple charges

Magnitude of electric field due multiple charges can be calculated using superposition principle.

It states that “The total electric field at a point P is the vector sum of the fields at P due to each point charge in the charge distribution.”

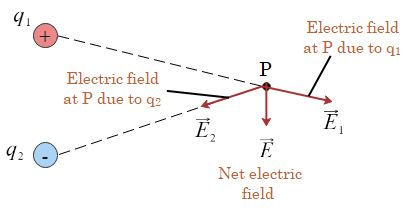
To explain this further let us consider the figure which shows two electric charges $q_1$ and $q_2$ and we have to find net electric field at point P due to these two charges.

According to principle of superposition

$\vec E = \frac{\vec F}{q’}=\vec{E_1}+\vec{E_2}$

If we have knowledge about the magnitude of charges and distance of point P from both these charges then we can use relation

$E=k\frac{Q}{{r}^{2}}$

Where $k=\frac{1}{4\pi\epsilon_0}=9.0\times 10^9 N\cdot m^/C^2$

To estimate the resultant field, we must calculate the electric field for each charge separately and then add them together.

Let us now understand this with the help of a problem.

Solved Example 2

Two point charges $q_A=3\mu C$ and $q_B=-3\mu C$ are placed at 20 cm apart in vacuum. What would be the electric field at the mid point $O$ of the line $AB$ joining the two charges?

Solution

Step- 1 Figure out what is requited

The question asked us to find magnitude of electric field at the center of line joining both the charges.

Step- 2 Figure out information given in the question.

We are provided the magnitude of the charge as well as the distance between both the charges

${q_A} = 3\mu C = 3 \times {10^{ – 6}}C$

${q_B} = -3\mu C = 3 \times {10^{ – 6}}C$

$r=20 cm = 0.2m$ we have to convert $r$ given in cm to m.

Let $0$ be the mid point of the line as shown below in the figure

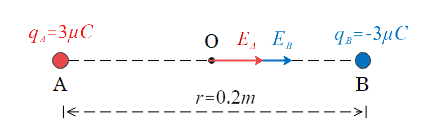
Then,

$OA=OB=\frac{r}{2}=\frac{0.2}{2}=0.1m$

Step- 3 Find out the way to solve problem

We will use the relation

$E=k\frac{Q}{{r}^{2}}$

To find the magnitude of electric field.

Step 4- Solve the problem

First we will calculate electric field at point O due to $q_A$

$E_A=k\frac{|q_A|}{(OA)^2}=9\times 10^9\times \frac{3 \times {10^{-6}}}{(0.1)^2}=2.7\times 10^6 N/C$

Acting along OB

Next we will calculate electric field at point O due to $q_B$

$E_B=k\frac{|q_B|}{(OB)^2}=9\times 10^9\times \frac{3 \times {10^{-6}}}{(0.1)^2}=2.7\times 10^6 N/C$

Acting along OB

Now since $E_A$ and $E_B$ are acting along same direction the angle between them is $\theta = 0\, radians$ and $coso = 1$

$|E| = \sqrt {E_A^2 + E_B^2 + 2{E_1}{E_2}cos\theta }$

$= \sqrt {E_A^2 + E_B^2 + 2{E_1}{E_2}}$

$= |{E_A}| + |{E_B}|$

Therefore net magnitude of electric field at point O due to two charges $q_A$ and $q_B$ would be,

$E=E_A+E_B=2.7\times 10^6+2.7\times 10^6 = 5.4\times 10^6 N/C$

Note:- If $E_A$ and $E_B$ acts along opposite direction the angle between them is $\theta = \pi \, radians$ and in that case $|E| = |{E_A}| – |{E_B}|$