In this article, we will derive the first equation of motion by graphical method.
The formula for the first equation of motion
The first equation of motion is given by the relation
\(v=u+at\)
Where
$v$= final velocity
$u$= initial velocity
$a$= acceleration
$s$= distance traveled
Let us now derive the first equation of motion v=u+at graphically. Before going any further it is important to note that this equation along with other kinematics equations of motion are valid for objects moving with uniform acceleration.
Derivation of 1st equation of motion by graphical method
The first equation of motion can be derived using a velocity-time graph for the moving object with an initial velocity of $u$, final velocity \(v\), and acceleration \(a\).
Here we are looking to find the velocity of a moving object at any time $t\) when we have knowledge of its initial velocity and acceleration. The reason we are using a velocity-time graph, in this case, is because it relates all these parameters. Also, the slope of the velocity-time graph tells us about the acceleration of the moving object. To find the first equation of motion consider the graph shown below in the figure.
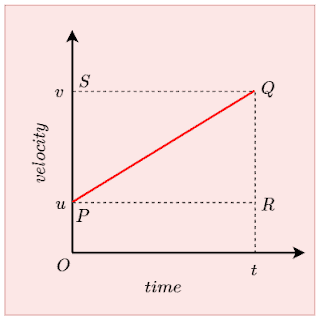
From this graph, we can easily see that
\(OP=u\) represents initial velocity of the object at time \(t=0\)
\(OS=v\) represents the final velocity of the object at time \(t\)
\(PR\) is time \(t\) during which motion takes place.
Now from this graph
\(a=\frac{QR}{PR}=\frac{SP}{PR}\)
\(SP=a.PR=at\)
As
\(OS=OP+PS\)
Substituting various values we get
\(v=u+at\)
Note on the first equation of motion
- This equation is the relation among initial velocity \((u)$, final velocity $(v)$, acceleration $(a)\) and time $(t)$.
- In lots of problems, the object starts motion from rest with zero initial velocity. In such cases, if we have knowledge about two kinematics quantities we can easily find the third quantity.