In this article, we will learn about the Calculation of electric fields from potential. We will also Derive the relation between electric field and electric potential. Electrical potential and the electrical field are complex but very important topics in electrostatics. Sometimes students get confused between these two quantities. Although both electric field and potential are quantities related to electrostatics there are many differences between them. The electric field is a vector quantity and electric potential on the other hand is a scalar quantity.
We will first cover a general overview of both topics and then discuss how to calculate voltage from the electrical field.
Important Terms and definitions
Electric Potential
Electric potential is the work done per unit test charge by an external agent in moving the test charge from one point to another point under a constant electric field. Since the potential energy is a scalar quantity, the electric potential is also a scalar quantity. The SI unit for electrical potential is Volt (V). Mathematically it is represented as,
$V = \frac{W}{Q}$
Where,
$V =$ Electrical potential in Volts
$W =$ Work done in joules
$Q =$ Electric Charge in coulombs
Electrical potential due to a point charge
The electric potential at a point in an electric field is defined as the amount of work done to bring a unit positive electric charge from infinity to that point.
$V = \frac{Q}{4\pi \epsilon_0 r}$
Where,
Distance between charge and the point $= r$
The source charge $= Q$
Coulomb’s constant = $\frac{1}{4\pi \epsilon_0 r}$
If one point has an electric potential of 5 volts, we can say that it takes 5 joules of work to bring a one-coulomb charge from infinity to that point.
Electric Potential Difference
The electrical potential difference is defined as the amount of work required to move a unit charge from one point to another point in an electric field. It can also be defined as the difference between the electric potentials of the two charged particles.
The SI unit for the electric potential difference is volt (V).
Thus, the potential difference between two points is said to be one volt, if one-joule work is done in moving a unit charge from one point to another.
For example, consider two-unit point charges A and B with electric potential 10 volts and 3 volts respectively. Then, 7 joules work is required to move unit charge B to the location of charge A.
Electric Field
The electric field is a physical field that surrounds an electrically charged particle. In this field, the charged particles exert electromagnetic force on all the other charged particles, either attracting or repelling them.
The electric field is defined at each point in space as the force per unit charge that would be experienced by a test charge if held at that point.
The derived SI units for the electric field are volts per meter (V/m), which is equivalent to Newton per Coulomb (N/C).
Calculation of electric field from potential
To calculate voltage from the electric field intensity let us first derive the relation between electric field and electric potential
Derive the relation between electric field and electric potential
By definition, the potential difference between two points $B$ and $A$ is given by
$V_B-V_A=-\int_A^B{\vec E \cdot \vec {dr}}$
Here, $dr $ denotes the small distance over which the unit positive charge is moved. If the electric field between these points is known, the above relationship can be utilized to compute the potential difference between the two points.
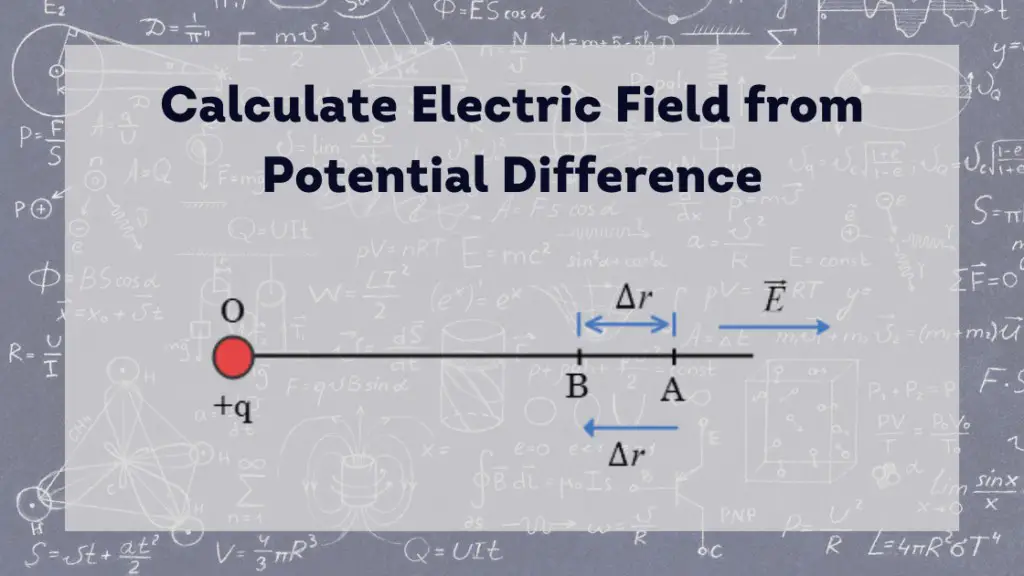
In the electric field of charge $+q$ placed at point O, consider two nearby locations $A$ and $B$ as shown in Figure below. Let points A and B be separated by $\Delta r$ (i.e. $AB = \Delta r$) by a small distance. The electric field intensity between points $A$ and $B$ remains constant since they are very close to each other.
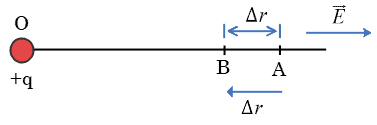
By definition, the potential difference between point $B$ and $A$ is equal to work done in moving unit positive charge from $A$ to $B$. So,
$\Delta V=\vec E \cdot \Delta \vec r=E\Delta r\cos 180^0=-E\Delta r$
The angle between $\vec E$ and $\vec r$ is $180^0$ because they act along the same line of action but in opposite direction.
Therefore,
$E=-\frac{\Delta V}{\Delta r}$
If we bring points $A$ and $B$ so close to each other such that $\Delta r \rightarrow 0$, then the above expression may be given in calculus form, i.e,
$E=-\frac{dV}{dr}$
The negative sign shows that the direction of the electric field is in the direction of decreasing potential.
This quantity $dv/dr$ is the rate of change of electric potential with the distance and is called potential gradient. Hence
the electric field at any point is equal to the negative of the potential gradient at that point.
There is a benefit to expressing electric field in terms of $V$ (potential). Because $V$ is a scalar quantity, analyzing the electric field becomes easier. Furthermore, electric potential gives an energy concept that aids in the solution of many problems. So, If the electric potential at each point in a region of space is known, the electric field could be calculated from the potential since electric field $E=-\frac{dV}{dr}$.
Calculating electric field from potential
Let us calculate voltage from the electric field intensity with the help of an example,
Example 1:- The Electric Potential $V$ at any point $(x,y,z)$ in Space is Given by $V=3x^2$ Volts, then the Electric Field at point Point $(2,1,2)$ is?
Solution:- According to question, the potential at any point $(x,y,z)$ is given by relation $V=3x^2$.
Here it is important to note that potential is only a function of $x$ so, the electric field would be the gradient of potential (V) in the x-direction such that $E=−\frac{dV}{dx}$. Here, the rate of change in potential of the test charge as it moves in the x-direction gives the value of the electric field.
We have to find the electric field $E$ at $(2,1,2)$.
We know that,
⇒ $E=−\frac{dV}{dx}$
⇒ $E=−\frac{d(3x^2)}{dx}=6x$
At $x=2$, $E = 6 \times (2) = 12 V/m$
Therefore, the electric field $E$ at $(2,1,2)$ is $12 V/m$.
Related Articles
